gileCAD

Le calcul vectoriel avec AutoLISP

Introduction

Dans AutoLISP, rien ne distingue un point (une position dans l'espace) d'un vecteur (un déplacement), or géométriquement, il s'agit bien de deux concepts radicalement différents.
Tous deux sont identiquement définis pas une liste de 3 nombres (ou 2 en 2D) définissant leurs coordonnées X, Y et Z dans un repère orthonormé (système de coordonnées).
Seule l'utilisation qui en est faite dans le programme permet de distinguer s'il s'agit d'un point, d'un vecteur ou encore d'une liste de nombres servant à tout autre chose.

Les codes de cet article sont adaptés de la bibliothèque MathGeom au bas de la page AutoLISP.

Point et vecteurs

Soient deux points distincts A et B. Le vecteur V de A à B correspond au déplacement (translation) du point A en B.

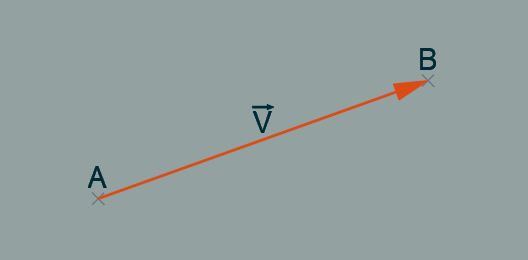
On calcule les coordonnées du vecteur V en soustrayant les coordonnées respectives de A à celle de B.

    x_B - x_A
V : y_B - y_A
    z_B - z_A

        
;; gc:GetVector
;; Retourne le vecteur de p1 à p2
;;
;; Arguments
;; p1, p2 : 2 points
(defun gc:GetVector (p1 p2) (mapcar '- p2 p1))

Norme d'un vecteur

Un vecteur est caractérisé par sa direction, son sens et sa norme (sa longueur).
On obtient facilement la longueur d'un vecteur avec la fonction distance :

        
;; gc:VecLength
;; Retourne la norme (longueur) du vecteur
;;
;; Argument
;; v : un vecteur
(defun gc:VecLength (v) (distance '(0. 0. 0.) v))

Vecteur unitaire

Il est souvent intéressant d'obtenir le vecteur unitaire (de norme 1.0) d'un vecteur :

        
;; gc:GetNormal
;; Retourne le vecteur unitaire d'un vecteur
;;
;; Argument
;; v : un vecteur
(defun gc:GetNormal (v)
  ((lambda (l)
     (if (/= 0 l)
       (mapcar (function (lambda (x) (/ x l))) v)
     )
   )
    (distance '(0. 0. 0.) v)
  )
)

Calcul vectoriel

Le calcul vectoriel est un ensemble d'opérations effectuées sur des vecteurs.
Ces opérations permettent de résoudre des problèmes géométriques en les ramenant à des opérations sur les nombres (les coordonnées des vecteurs).

Déplacement de point et somme de vecteurs

Si ajouter un point à un autre n'a aucun sens, on peut ajouter un vecteur à un point, ce qui correspond à déplacer le point de la valeur du vecteur : ajouter le vecteur V au point A donne le point B.

        x_A + x_V
A + V : y_A + y_V
        z_A + z_V

On peut également ajouter un vecteur à un autre : la somme des vecteurs U et V donne le vecteur U+V.

        x_U + x_V
U + V : y_U + y_V
        z_U + z_V

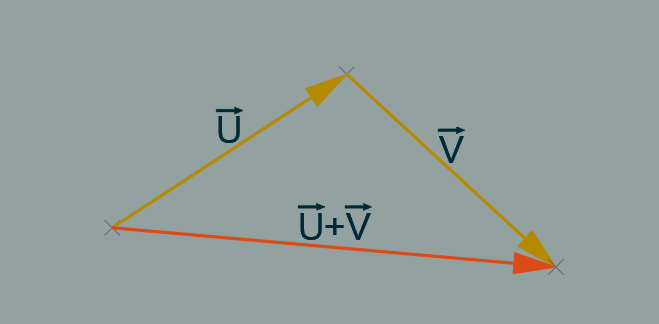
Avec AutoLISP ces deux opérations sont identiques : on ajoute les coordonnées respectives du point et du vecteur dans le premier cas, des deux vecteurs dans le second.

        
;; déplacement du point a en b
(setq b (mapcar '+ a v))

;; somme des vecteurs u et v
(setq w (mapcar '+ u v))

Par contre, géométriquenment, il s'agit bien de deux opérations différentes.
Dans le premier cas le résultat est un point (le point passé en argument déplacé de la valeur du vecteur).
Dans le second cas, le résultat est un vecteur (la résultante des deux vecteurs passé en argument).
Encore une fois seul le contexte dans le programme permet de distinguer le premier du second cas.

Multiplication d'un vecteur par un scalaire

En multipliant un vecteur par un nombre (scalaire), on modifie proportionnellement sa longueur.
On obtient un vecteur d'une longueur donnée en multipliant le vecteur unitaire par cette longueur.

        k * x_V
k * V : k * y_V
        k * z_V

        
;; gc:ScaleVector
;; Multiplie le vecteur par un scalaire
;;
;; Arguments
;; v : un vecteur
;; s : un nombre
(defun gc:ScaleVector (v s)
  (mapcar (function (lambda (x) (* x s))) v)
)

Produit scalaire de deux vecteurs

Le produit scalaire de deux vecteurs renvoie un nombre réel (scalaire).
Ce nombre est égal à 0 si les vecteurs sont perpendiculaires ou si un des deux vecteurs est nul (0, 0, 0).
Il est positif si l'angle entre les vecteurs est aigu, négatif si l'angle est obtus.


U · V = x_U * x_V + y_U * y_V + z_U * z_V

        
;; gc:DotProduct
;; Retourne le produit scalaire de deux vecteurs
;;
;; Arguments
;; v1, v2 : deux vecteurs
(defun gc:DotProduct (v1 v2) (apply '+ (mapcar '* v1 v2)))

Produit vectoriel de deux vecteurs

Le produit vectoriel de deux vecteurs est le vecteur perpendiculaire à ces deux vecteurs. Il est orienté en fonction de la "règle de la main droite".
Si A, B et C sont 3 points distincts, le produit vectoriel des vecteurs U de A à B et V de A à C est le vecteur normal du plan défini par A, B et C.
La norme (longueur) du produit vectoriel est égale au double de l'aire du triangle.

        y_U * z_V - z_U * y_V
U ˄ V : z_U * x_V - x_U * z_V
        x_U * y_V - y_U * x_V

        
;; gc:CrossProduct
;; Retourne le produit vectoriel (vecteur) de deux vecteurs
;;
;; Arguments
;; v1, v2 : deux vecteurs
(defun gc:CrossProduct (v1 v2)
  (list	(- (* (cadr v1) (caddr v2)) (* (caddr v1) (cadr v2)))
	(- (* (caddr v1) (car v2)) (* (car v1) (caddr v2)))
	(- (* (car v1) (cadr v2)) (* (cadr v1) (car v2)))
  )
)

Exemples pratiques d'utilisation

Ces opérations facilitent la définition de fonctions géométriques plus complexes.

Aire algébrique du triangle (2D)

Utilisation de la coordonnée Z du produit vectoriel pour calculer l'aire algébrique d'un triangle.
Ce calcul ne fait intervenir que les coordonnées X et Y des points, il n'est donc valide qu'en 2D.
Cette aire est négative si les points sont en sens horaire.

        
;; gc:AlgebraicArea
;; Retourne l'aire algébrique du triangle p1 p2 p3
;;
;; Arguments
;; p1, p2, p3 : 3 points 2D
(defun gc:AlgebraicArea (p1 p2 p3)
  ((lambda (v1 v2)
     (/ (- (* (car v1) (cadr v2)) (* (cadr v1) (car v2))) 2.)
   )
    (gc:GetVector p1 p2)
    (gc:GetVector p1 p3)
  )
)

Vecteur normal du plan défini par 3 points

Utilisation du produit vectoriel pour calculer le vecteur normal d'un plan défini par 3 points (vecteur perpendiculaire au plan).

        
;; gc:Normal3Points
;; Retourne le vecteur normal du plan défini par p1, p2 et p3
;;
;; Arguments
;; p1, p2, p3 : 3 points
(defun gc:Normal3Points (p1 p2 p3)
  (gc:CrossProduct (gc:GetVector p1 p2) (gc:GetVector p1 p3))
)

L'aire du triangle est égale à la moitié de la norme du vecteur normal.

        
;; Aire du triangle p1, p2, p3.
(/ (gc:VecLength (gc:Normal3Points p1 p2 p3)) 2.)

Segments parallèles

Utilisation du produit vectoriel pour évaluer si deux segments sont parallèles.
Les segments sont parallèles si le produit vectoriel de leurs vecteurs directionnels est le vecteur nul.

        
;; gc:Parallelp
;; Evalue si les segments p1 p2 et p3 p4 sont parallèles
;;
;; Arguments
;; p1 : un point sur le premier segment
;; p2 : un autre point sur le premier segment
;; p3 : un point sur le second segment
;; p4 : un autre point sur le second segment
(defun gc:Parallelp (p1 p2 p3 p4)
  (equal '(0. 0. 0.)
	 (gc:CrossProduct (gc:GetVector p1 p2) (gc:GetVector p3 p4))
	 1e-9
  )
)

Segments perpendiculaires

Utilisation du produit scalaire pour évaluer si deux segments sont perpendiculaires.
Les segments sont perpendiculaires si le produit scalaire de leurs vecteurs directionnels est égal à 0.

        
;; gc:Penpendicularp
;; Evalue si les segments p1 p2 et p3 p4 sont perpendiculaires
;;
;; Arguments
;; p1 : un point sur le premier segment
;; p2 : un autre point sur le premier segment
;; p3 : un point sur le second segment
;; p4 : un autre point sur le second segment
(defun gc:Penpendicularp (p1 p2 p3 p4)
  (equal (gc:DotProduct (gc:GetVector p1 p2) (gc:GetVector p3 p4))
	 0
	 1e-9
  )
)

Projection d'un point sur une droite

Utilisation du produit scalaire pour trouver la projection d'un point sur une droite.
Algorithme :
Soient P1 et P2 deux points sur la droite, U le vecteur unitaire de P1 à P2 et V le vecteur de P1 à PT.
La projection de PT sur la droite (P1 P2) correspond au déplacement de P1 par U multiplié par le produit scalaire de U et V.

        
;; gc:ProjectOnLine
;; Retourne la projection de pt sur la droite p1 p2
;;
;; Arguments
;; pt : le point à projeter
;; p1 : un point sur la droite
;; p2 : un point sur la droite
(defun gc:ProjectOnLine (pt p1 p2)
  ((lambda (u v)
     (mapcar '+ p1 (gc:ScaleVector u (gc:DotProduct u v)))
   )
    (gc:GetNormal (gc:GetVector p1 p2))
    (gc:GetVector p1 pt)
  )
)

Intersection d'une droite et d'un plan

Utilisation du produit scalaire pour trouver l'intersection d'une droite et d'un plan.
Algorithme :
Soient P1 et P2 deux points sur la droite, V le vecteur de P1 à P2, N le vecteur normal du plan et O un point sur le plan, .
On calcule S1, produit scalaire de N et de V.
Un résultat égal à 0 signifie que les vecteurs sont perpendiculaires, autrement dit que le segment est parallèle au plan : il n'y a pas d'intersection.
On calcule S2, produit scalaire de N et du vecteur du point P1 au point O.
Le scalaire S est égal à S2 divisé par S1.
Le point d'intersection entre la droite (P1, P2) et le plan est égal au point P1 déplacé par le vecteur V multiplié par S (P1 + V * S).
Si S est compris entre 0 et 1 cela signifie que le point d'intersection appartient au segment.

        
;; gc:IntersLinePlane
;; Retourne le point d'intersection de la droite définie par p1 p2
;; avec le plan défini pas un point et son vecteur normal
;;
;; Arguments
;; p1 : un point sur la droite
;; p2 : un autre point sur la droite
;; norm : le vecteur normal du plan
;; org : un point sur le plan de projection
;; onSeg : si T, le point d'intersection doit être sur le segment p1, p2
;;         si nil, le segment est prolongé
(defun gc:IntersLinePlane (p1 p2 norm org onSeg / scl)
  (if
    (and
      (/= 0. (setq scl (gc:DotProduct norm (gc:GetVector p1 p2))))
      (or
	(<= 0.
	    (setq scl (/ (gc:DotProduct norm (gc:GetVector p1 org)) scl))
	    1.
	)
	(not onSeg)
      )
    )
     (mapcar '+ p1 (gc:ScaleVector (gc:GetVector p1 p2) scl))
  )
)